|
|
|
|
|
 |
|
|
 |
Tipos de geometría
Entre los tipos de geometría más destacadas se encuentran:
La geometría euclidiana
Ç] es aquella que estudia las propiedades del plano y el espacio tridimensional. En ocasiones los matemáticos usan el término para englobar geometrías de dimensiones superiores con propiedades similares. Sin embargo, con frecuencia, geometría euclidiana es sinónimo de geometría plana.

Fragmento de Los elementos de Euclides, escrito en papiro, hallado en el yacimiento de Oxirrinco (Oxyrhynchus), Egipto.
- Desde un punto de vista historiográfico, la geometría euclidiana es aquella geometría que postuló Euclides, en su libro "Los elementos", dejando al margen las aportaciones que se hicieron posteriormente –desde Arquímedes hasta Steiner.
- Según la contraposición entre método sintético y método algebraico-analítico, la geometría euclidiana sería, precisamente, el estudio por métodos sintéticos de los invariantes de un espacio vectorial real de dimensión 3 dotado de un producto escalar muy concreto (el frecuentemente denominado producto escalar habitual).
- Según el Programa de Erlangen, la geometría euclidiana sería el estudio de los invariantes de las isometrías en un espacio euclidiano (espacio vectorial real de dimensión finita, dotado de un producto escalar).[2]
Geometría plana
La geometría plana es una parte de la geometría que trata de aquellos elementos cuyos puntos están contenidos en un plano. La geometría plana está considerada parte de la geometría euclidiana, pues ésta estudia los elementos geométricos a partir de dos dimensiones.
Una parte importante de la geometría plana son las construcciones con regla y compás.
Geometría espacial
La geometría espacial o geometría del espacio es la rama de la geometría que se ocupa de las propiedades y medidas de las figuras geométricas en el espacio tridimensional o espacio euclídeo. Entre estas figuras, también llamadas sólidos, se encuentran el cono, el cubo, el cilindro, la pirámide, la esfera, el prisma, los poliedros regulares (los sólidos platónicos, convexos, y los sólidos de Kepler-Poinsot, no convexos) y otros poliedros.
La geometría del espacio amplía y refuerza las proposiciones de la geometría plana, y es la base fundamental de la trigonometría esférica, la geometría analítica del espacio, la geometría descriptiva y otras ramas de las matemáticas. Se usa ampliamente en matemáticas, en ingeniería y en ciencias naturales.
Llamamos cuerpos geométricos a las figuras que se han de representar en el espacio tridimensional. Los cuerpos geométricos ocupan siempre un espacio.
Asimismo, los cuerpos que están huecos pueden albergar en su interior otros cuerpos en una cantidad que recibe el nombre de capacidad. Existe una relación directa entre la capacidad de un cuerpo y el volumen que éste ocupa.
La geometría espacial se basa en un sistema formado por tres ejes (X,Y,Z):
- Ortogonales (perpendiculares 2 a 2)
- Normalizados (las longitudes de los vectores básicos de cada eje son iguales)
- Dextrógiros (el tercer eje es producto vectorial de los otros 2)
Geometría analítica
Se conoce como geometría analítica al estudio de ciertos objetos geométricos mediante técnicas básicas del análisis matemático y del álgebra en un determinado sistema de coordenadas. Se podría decir que es el desarrollo histórico que comienza con la geometría cartesiana y concluye con la aparición de la geometría diferencial con Gauss y más tarde con el desarrollo de la geometría algebraica.
Los dos problemas fundamentales de la geometría analítica son:
1.- Dado el lugar geométrico en un sistema de coordenadas, obtener su ecuación.
2.- Dada la ecuación en un sistema de coordenadas, determinar la gráfica o lugar geométrico de los puntos que la cumplen.
Lo novedoso de la Geometría Analítica es que permite representar figuras geométricas mediante fórmulas del tipo f(x,y) = 0, donde f representa una función u otro tipo de expresión matemática. En particular, las rectas pueden expresarse como ecuaciones polinómicas de grado 1 (v.g.: 2x + 6y = 0) y las circunferencias y el resto de cónicas como ecuaciones polinómicas de grado 2 (v.g.: la circunferencia x2 + y2 = 4, la hipérbola xy = 1 ).
Construcciones fundamentales
En un sistema de coordenadas cartesianas, un punto del plano queda determinado por dos números, llamados "abscisa" y "ordenada" del punto. Mediante ese procedimiento a todo punto del plano corresponden siempre dos números reales ordenados (abscisa y ordenada), y recíprocamente, a un par ordenado de números corresponde un único punto del plano. Consecuentemente el sistema cartesiano establece una correspondencia biunívoca entre un concepto geométrico como es el de los puntos del plano y un concepto algebraico como son los pares ordenados de números. Esta correspondencia constituye el fundamento de la Geometría Analítica.
Con la Geometría Analítica se puede determinar figuras geométricas planas por medio de ecuaciones e inecuaciones con dos incógnitas. Éste es un método alternativo de resolución de problemas, o cuando menos nos proporciona un nuevo punto de vista con el cual poder atacar el problema.
Localización de un punto en el plano cartesiano
En un plano traza dos rectas perpendiculares (ejes) —que por convenio se trazan de manera que una de ellas sea horizontal y la otra vertical—, y cada punto del plano queda unívocamente determinado por las distancias de dicho punto a cada uno de los ejes, siempre y cuando se dé también un criterio para determinar sobre qué semiplano determinado por cada una de las rectas hay que tomar esa distancia, criterio que viene dado por un signo. Ese par de números, las coordenadas, quedará representado por un par ordenado (x,y), siendo x la distancia a uno de los ejes (por convenio será la distancia al eje vertical) e y la distancia al otro eje (al horizontal).
En la coordenada x, el signo positivo (que suele omitirse) significa que la distancia se toma hacia la derecha del eje horizontal (eje de las abscisas), y el signo negativo (nunca se omite) indica que la distancia se toma hacia la izquierda. Para la coordenada y, el signo positivo (también se suele omitir) indica que la distancia se toma hacia arriba del eje vertical (eje de ordenadas), tomándose hacia abajo si el signo es negativo (tampoco se omite nunca en este caso). A la coordenada x se la suele denominar abscisa del punto, mientras que a la y se la denomina ordenada del punto.
Los puntos del eje de abscisas tienen por lo tanto ordenada igual a 0, así que serán de la forma (x,0), mientras que los del eje de ordenadas tendrán abscisa igual a 0, por lo que serán de la forma (0,y).
El punto donde ambos ejes se cruzan tendrá por lo tanto distancia 0 a cada uno de los ejes, luego su abscisa será 0 y su ordenada también será 0. A este punto —el (0,0)— se le denomina origen de coordenadas.
Ecuaciones de la recta en el plano
Una recta es el lugar geométrico de todos los puntos en el plano tales que, tomados dos cualesquiera de ellos, el cálculo de la pendiente resulta siempre igual a una constante.
La ecuación general de la recta es de la forma:
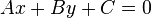
cuya pendiente es m = -A/B y cuya ordenada al origen es b = -C/B.
Una recta en el plano se representa con la función polinómica de primer grado de la forma:

como expresión general, Esta es conocida como ecuación pendiente-ordenada al origen y podemos distinguir dos casos particulares. Si una recta no corta a uno de los ejes, será porque es paralela a él. Como los dos ejes son perpendiculares, si no corta a uno de ellos forzosamente ha de cortar al otro (siempre y cuando la función sea continua para todos los reales). Tenemos pues tres casos:
-
|
|
|
|
| Rectas oblicuas. |
Rectas horizontales. |
Rectas verticales. |
- Rectas verticales, estas rectas no cortan al eje de ordenadas y son paralelas a dicho eje y se denominan rectas verticales. El punto de corte con el eje de abscisas es el punto (x0,0). La ecuación de dichas rectas es:

- Rectas horizontales, estar rectas no cortan al eje de las abscisas y, por tanto, son paralelas a dicho eje y se denominan rectas horizontales. El punto de corte con el eje de ordenadas es el punto (0,y0). La ecuación de dichas rectas es:

- Rectas oblicuas. Cualquier otro tipo de recta recibe el nombre de recta oblicua. En ellas hay un punto de corte con el eje de abscisas (a,0) y otro punto de corte con el eje de ordenadas (0,b). El valor a recibe el nombre de abscisa en el origen, mientras que el b se denomina ordenada en el origen.
Secciones cónicas

Los tres ejemplos de intersección de un plano con un cono: parábola ( A), elipse ( B) e hipérbola ( C).
El resultado de la intersección de la superficie de un cono, con un plano, da lugar a lo que se denominan secciones cónicas, que son: la parábola, la elipse (la circunferencia es un caso particular de elipse) y la hipérbola.
- La parábola es el lugar geométrico de todos los puntos que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.
Una parábola (Figura A) cuyo eje de simetría sea paralelo al eje de abcisas se expresa mediante la ecuación:

- Elipse es el lugar geométrico de los puntos tales que la suma de sus distancias a dos puntos fijos llamados focos es siempre igual a una constante positiva, e igual a la distancia entre los vértices.
Una elipse (Figura B) centrada en los ejes, con longitudes de semieje a y b viene dada por la expresión:

- Si los dos ejes son iguales y los llamamos c:
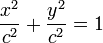
- el resultado es una circunferencia:

- La hipérbola es el lugar geométrico de los puntos tales que el valor absoluto de la diferencia (resta) de sus distancias a dos puntos fijos llamados focos es siempre igual a una constante positiva, e igual a la distancia entre los vértices.
La hipérbola (Figura C) tiene por expresión:
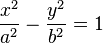
Construcciones en el espacio tridimensional

Un toro, ejemplo de superficie tridimensional.
Los razonamientos sobre la construcción de los ejes coordenados son igualmente válidos para un punto en el espacio y una terna ordenada de números, sin más que introducir una tercera recta perpendicular a los ejes X e Y: el eje Z.
Sin embargo no hay análogo al importantísimo concepto de pendiente de una recta. Una única ecuación lineal del tipo:
ax + by + cz = 0
Representa en el espacio un plano. Si se pretende representar mediante ecuaciones una recta en el espacio tridimensional necesitaremos especificar, no una, sino dos ecuaciones lineales como las anteriores. De hecho toda recta se puede escribir como interesección de dos planos. Así una recta en el espacio podría quedar representada como:

Es importante notar que la representación anterior no es única, ya que una misma recta puede expresarse como la intersección de diferentes pares de planos. Por ejemplo los dos pares de ecuaciones:
Clasificación de la geometría analítica dentro de la geometría
Desde el punto de vista de la clasificación de Klein de las geometrías (el Programa de Erlangen), la geometría analítica no es una geometría propiamente dicha.
Desde el punto de vista didáctico, la geometría analítica resulta un puente indispensable entre la geometría euclidiana y otras ramas de la matemática y de la propia geometría, como son el propio análisis matemático, el álgebra lineal, la geometría afín, la geometría diferencial o la geometría algebraica.
Historia de la geometría analítica
Existe una cierta controversia sobre la verdadera paternidad de este método. Lo único cierto es que se publica por primera vez como "Geometría analítica", apéndice al Discurso del método, de Descartes, si bien se sabe que Pierre de Fermat conocía y utilizaba el método antes de su publicación por Descartes. Aunque Omar Khayyam ya en el siglo XI utilizara un método muy parecido para determinar ciertas intersecciones entre curvas, es imposible que alguno de los citados matemáticos franceses tuvieran acceso a su obra.
El nombre de geometría analítica corrió parejo al de geometría cartesiana, y ambos son indistinguibles. Hoy en día, paradójicamente, se prefiere denominar geometría cartesiana al apéndice del Discurso del método, mientras que se entiende que geometría analítica comprende no sólo a la geometría cartesiana (en el sentido que acabamos de citar, es decir, al texto apéndice del Discurso del método), sino también todo el desarrollo posterior de la geometría que se base en la construcción de ejes coordenados y la descripción de las figuras mediante funciones —algebraicas o no— hasta la aparición de la geometría diferencial de Gauss (decimos "paradójicamente" porque se usa precisamente el término "geometría cartesiana" para aquello que el propio Descartes bautizó como "geometría analítica"). El problema es que durante ese periodo no existe una diferencia clara entre geometría analítica y análisis matemático —esta falta de diferencia se debe precisamente a la identificación hecha en la época entre los conceptos de función y curva—, por lo que resulta a veces muy difícil intentar determinar si el estudio que se está realizando corresponde a una u otra rama.
La geometría diferencial de curvas sí que permite un estudio mediante un sistema de coordenadas, ya sea en el plano o en el espacio tridimensional. Pero en el estudio de las superficies, en general, aparecen serios obstáculos. Gauss salva dichos obstáculos creando la geometría diferencial, y marcando con ello el fin de la geometría analítica como disciplina. Es con el desarrollo de la geometría algebraica cuando se puede certificar totalmente la superación de la geometría analítica.
Es de puntualizar que la denominación de analítica dada a esta forma de estudiar la geometría provocó que la anterior manera de estudiarla (es decir, la manera axiomático-deductiva, sin la intervención de coordenadas) se terminara denominando, por oposición, geometría sintética, debido a la dualidad análisis-síntesis.
Actualmente el término geometría analítica sólo es usado en enseñanzas medias o en carreras técnicas en las que no se realiza un estudio profundo de la geometría.
Geometría diferencial
En matemática, la geometría diferencial es el estudio de la geometría usando las herramientas del análisis matemático. Los objetos de estudio de este campo son las variedades diferenciables (tal y como la topología diferencial) tanto como las nociones de conexión y curvatura (que no se estudia en la topología diferencial).
Las aplicaciones modernas de la geometría diferencial han dado el estado del arte que goza la física.
Geometría proyectiva
Se llama geometría proyectiva a una estructura matemática que estudia las incidencias de puntos y rectas sin tener en cuenta la medida. A menudo se usa esta palabra también para hablar de la teoría de la proyección que en realidad se llama geometría descriptiva
Breve reseña histórica
Gérard Desargues es el iniciador de la geometría proyectiva, pues fundamentó matemáticamente los métodos de la perspectiva que habían desarrollado los artistas del Renacimiento, y aunque su trabajo fue publicado en 1639, pasó desapercibido durante dos siglos (excepto dos teoremas), ensombrecido por la influyente obra de Descartes.
En el siglo XIX, la geometría proyectiva y la geometría hiperbólica, se establecieron dentro de las matemáticas, pero lo que acabó de enraizarlas, posiblemente, fue hallar un modelo analítico. Dentro del contexto de la geometría euclidiana-cartesiana se puede construir la geometría proyectiva, y si se acepta la primera, hay que admitir la segunda.
Este proceso finalizó definitivamente a principios del siglo XX, pues Einstein, apoyándose en los exhaustivos desarrollos geométricos de los matemáticos del siglo XIX, consiguió demostrar que, a gran escala, el universo se puede interpretar mejor con estas nuevas geometrías que con el rígido espacio euclidiano.
Punto de vista sintético
Desde el punto de vista sintético, la geometría proyectiva es una geometría que parte de los siguientes principios:
- Dos puntos definen una recta.
- Todo par de rectas se cortan en un punto (cuando dos rectas son paralelas decimos que se cortan en un punto del infinito conocido como punto impropio).
El quinto postulado de Euclides, de las paralelas, está implícito en estos dos principios ya que, dada una recta y un punto exterior, existirá una única paralela (el punto dado y el del infinito definen la paralela por el primer axioma. Nótese que en la geometría proyectiva, dos rectas paralelas por definición comparten un punto y esto no excluye que sean isomorfas con las paralelas euclídeas).
Como los axiomas de los que se parte son simétricos, si en cualquier teorema proyectivo se intercambian las palabras recta y punto se obtiene otro teorema igualmente válido. A estos teoremas se les llama duales.
El principio antes expuesto se conoce como Principio de Dualidad y fue enunciado por Poncelet en el siglo XIX. Muchos teoremas anteriores, como los de Pascal y Brianchon, son duales, aunque ningún matemático lo había notado hasta entonces.
Los teoremas de Pascal y Brianchon, aunque completamente válidos, se demostraron inicialmente en geometría euclidiana, basándose en los teoremas de Pappus y Menelao, que utilizan una métrica y por tanto no son válidos en geometrías de incidencia, como la proyectiva.
En principio se intentó buscar demostraciones alternativas de estos teoremas sin usar congruencia de segmentos. Hilbert demostró en 1899 que tal cosa es imposible y desde entonces suele incluirse el teorema del hexágono de Pappus como un axioma de la geometría proyectiva. Ello permite demostrar en proyectiva todo lo demostrable en euclídea sin tener que recurrir a una métrica.
Por no usar métricas en sus enunciados, se dice que la geometría proyectiva es una Geometría de incidencia.
Finalmente, hay que destacar que desde el punto de vista sintético, un espacio proyectivo consiste en un espacio afín al que hemos añadido un conjunto de puntos infinitos, de modo que cada par de rectas paralelas se cortan en uno de estos puntos.
Aplicaciones
Cuando hacemos isomorfas nuestras paralelas euclídeas con las rectas proyectivas que se cortan “en el infinito”, podemos extrapolar todo lo que demostremos en proyectiva a geometría euclidiana. La geometría proyectiva, más flexible que la euclidiana, se convierte con esto en una herramienta útil para enunciar muchos teoremas clásicos más sencillamente, e incluso simplificar las demostraciones, aunque no permite demostrar nada que no pueda demostrarse en euclidiana.
La geometría proyectiva puede entenderse, informalmente, como la geometría que se obtiene cuando nos colocamos en un punto, mirando desde ese punto. Esto es, cualquier línea que incide en nuestro "ojo" nos parece ser sólo un punto, en el Plano proyectivo, ya que el ojo no puede "ver" los puntos que hay detrás.
De esta forma, la geometría proyectiva también equivale a la proyección sobre un plano de un subconjunto del espacio en la geometría euclidiana tridimensional. Las rectas que salen del ojo del observador se proyectan sobre puntos. Los planos definidos por cada par de ellas se proyectan sobre rectas.
Esto es útil porque a veces los teoremas de geometría proyectiva no pueden demostrarse sólo con los axiomas de incidencia antes expuestos (Hilbert, 1899) y es necesario demostrarlos en geometría euclidiana y luego proyectar, como el Teorema de Desargues (o bien admitir el teorema de Papus anteriormente citado como axioma)
Punto de vista vectorial
La geometría proyectiva es el estudio del grupo de las proyectividades entre espacios proyectivos.
Sea K un cuerpo y V un K-espacio vectorial (no trivial). Las rectas vectoriales de V son aquellos conjuntos formados por los múltiplos escalares de los vectores no nulos, esto es, si  , , 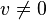 , la recta vectorial determinada por v es el conjunto , la recta vectorial determinada por v es el conjunto  . La recta vectorial determinada por v no es entonces otra cosa que el espacio generado por v, es decir, L(v). El espacio proyectivo P(V) asociado a V será el conjunto de todas las rectas vectoriales de V. . La recta vectorial determinada por v no es entonces otra cosa que el espacio generado por v, es decir, L(v). El espacio proyectivo P(V) asociado a V será el conjunto de todas las rectas vectoriales de V.
Es inmediato que si  , , 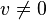 , entonces para cualquier , entonces para cualquier 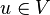 tal que u = βv con tal que u = βv con  , se cumple que las rectas vectoriales determinadas por u y por v coinciden, esto es, , se cumple que las rectas vectoriales determinadas por u y por v coinciden, esto es,  = =  . Ahí reside la esencia de un espacio proyectivo: consideramos sólo las direcciones, no los vectores concretos. Ante este hecho, para trabajar sólo con vectores y no con rectas vectoriales, se establece la siguiente relación, que resulta ser una relación de equivalencia: si . Ahí reside la esencia de un espacio proyectivo: consideramos sólo las direcciones, no los vectores concretos. Ante este hecho, para trabajar sólo con vectores y no con rectas vectoriales, se establece la siguiente relación, que resulta ser una relación de equivalencia: si  , diremos que u está relacionado con v (lo escribiremos como uRv) si existe un , diremos que u está relacionado con v (lo escribiremos como uRv) si existe un  de manera que v = λu. Al tomar el conjunto cociente V / R se obtiene otra forma de definir P(V). Los elementos del espacio proyectivo serían entonces las clases de equivalencia de los vectores de V mediante la relación de equivalencia R. de manera que v = λu. Al tomar el conjunto cociente V / R se obtiene otra forma de definir P(V). Los elementos del espacio proyectivo serían entonces las clases de equivalencia de los vectores de V mediante la relación de equivalencia R.
Aun puede darse otro paso más para comprender mejor éste tipo de espacios: si tomamos una base de V, como al tomar la recta vectorial generada por v exigimos que 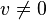 , alguna las coordenadas de v respecto de la base tomada ha de ser necesariamente no nula. Al multiplicar escalarmente el vector nulo por el inverso de esa coordenada no nula obtendremos otro vector de la misma recta vectorial, en el que ahora la coordenada no nula elegida va a valer 1. Como el nuevo vector está en la misma recta vectorial, su clase de equivalencia es la misma que la del vector antiguo, es decir, representa al mismo elemento del espacio proyectivo. , alguna las coordenadas de v respecto de la base tomada ha de ser necesariamente no nula. Al multiplicar escalarmente el vector nulo por el inverso de esa coordenada no nula obtendremos otro vector de la misma recta vectorial, en el que ahora la coordenada no nula elegida va a valer 1. Como el nuevo vector está en la misma recta vectorial, su clase de equivalencia es la misma que la del vector antiguo, es decir, representa al mismo elemento del espacio proyectivo.
Veamos en un ejemplo qué significa esto: Tomemos el espacio vectorial real  (con la base canónica) y el vector no nulo (con la base canónica) y el vector no nulo  . Denotaremos por . Denotaremos por ![[ (8, frac{pi}{3},0,2^{-15},sqrt{7}) ]](http://upload.wikimedia.org/math/f/7/9/f79557697cc6ca9fb1558295401c997f.png) a su clase de equivalencia mediante la relación R. Cuatro de las cinco coordenadas son no nulas, así que tenemos cuatro posibles maneras de realizar el proceso anterior: en el primer caso (dividiendo entre la primera coordenada, el a su clase de equivalencia mediante la relación R. Cuatro de las cinco coordenadas son no nulas, así que tenemos cuatro posibles maneras de realizar el proceso anterior: en el primer caso (dividiendo entre la primera coordenada, el  obtendríamos obtendríamos ![[(1,frac{pi}{24}, 0, 2^{-18},frac{sqrt{7}}{8})]](http://upload.wikimedia.org/math/4/a/6/4a6f11ae641c97ec12b4bfda178eea71.png) . Si en lugar de tomar la primera coordenada tomamos, por ejemplo, la quinta ( . Si en lugar de tomar la primera coordenada tomamos, por ejemplo, la quinta ( ), obtendríamos ), obtendríamos ![[ (frac{8}{sqrt{7}}, frac{pi}{3 sqrt{7}},0,frac{2^{-15}}{sqrt{7}} ,1) ]](http://upload.wikimedia.org/math/5/0/1/501881acdaa1b2fdeead5f9e4af0fc95.png) . Podríamos dividir las coordenadas del vector inicial . Podríamos dividir las coordenadas del vector inicial  entre las otras dos coordenadas no nulas, entre las otras dos coordenadas no nulas, 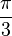 o 2 − 15, pero en todos los casos obtendríamos la misma clase de equivalencia, aunque las coordenadas no sean, numéricamente las mismas. En esta situación se dirá que o 2 − 15, pero en todos los casos obtendríamos la misma clase de equivalencia, aunque las coordenadas no sean, numéricamente las mismas. En esta situación se dirá que 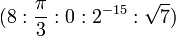 es la representación de la clase del vector es la representación de la clase del vector  en coordenadas homogéneas. Ha de quedar claro que en coordenadas homogéneas. Ha de quedar claro que 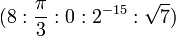 , ,  y y  son coordenadas homogéneas del mismo punto proyectivo. son coordenadas homogéneas del mismo punto proyectivo.
Geometría descriptiva
La geometría descriptiva es un conjunto de técnicas de carácter geométrico que permite representar el espacio tridimensional sobre una superficie bidimensional y, por tanto, resolver en dos dimensiones los problemas espaciales garantizando la reversibilidad del proceso a través de la adecuada lectura.
En la época actual se reconocen dos modelos: uno que considera la geometría descriptiva como un lenguaje de representación y sus aplicaciones, y otro que la sitúa como un tratado de geometría. Aunque no es exactamente lo mismo, su desarrollo ha estado asociado al de la Geometría proyectiva.
Breve reseña histórica
La geometría descriptiva, que posee el carácter de ciencia aplicada, ha tenido un largo proceso de desarrollo desde las incipientes representaciones trazadas en la edad de piedra. Los Elementos de Euclides, los estudios de Descartes en geometría analítica y la crucial aportación de Gaspard Monge a finales del siglo XVIII, quien la formula y la eleva a la condición de ciencia autónoma.
Desde la antigüedad, el hombre ha sentido siempre la necesidad de representar gráficamente el entorno que le rodea, como lo demuestran los dibujos encontrados en las cuevas prehistóricas, pero no es hasta el renacimiento cuando se intenta representar la profundidad.
Las nuevas necesidades de representación del arte y de la técnica empujan a ciertos humanistas a estudiar propiedades geométricas para obtener nuevos métodos que les permitan representar fielmente la realidad. Aquí se enmarcan figuras como Luca Paccioli, Leonardo da Vinci, Alberto Durero, Leone Battista Alberti, Piero della Francesca y muchos otros.
Todos ellos, al descubrir la perspectiva y la sección crean la necesidad de sentar las bases formales en la que se asiente la nueva forma de Geometría que ésta implica: la Geometría proyectiva, cuyos principios fundamentales aparecen de la mano de Gérard Desargues en el siglo XVII. Esta nueva geometría también fue estudiada por Blaise Pascal o por de la Hire, pero debido al gran interés suscitado por la Geometría Cartesiana y sus métodos, no alcanzó tanta difusión.
El posterior desarrollo de la técnica hizo necesario aplicar las teorías matemáticas a la práctica, proceso que culminó en 1795 con la publicación de la obra de Gaspard Monge «Geometría descriptiva».
La geometría
La geometría es la parte de las matemáticas que estudia las propiedades y las medidas de las figuras en el plano o en el espacio.
Se distinguen varias clases de geometría:
- Geometría algorítmica: aplicación del álgebra a la geometría para resolver por medio del cálculo ciertos problemas.
- Geometría analítica: estudio de figuras que utiliza un sistema de coordenadas y los métodos del análisis matemático.
- Geometría plana: parte de la geometría que considera las figuras cuyos puntos están todos en un plano.
- Geometría del espacio: la que considera las figuras cuyos puntos no están todos en un mismo plano.
- Geometría descriptiva: la que tiene por objeto resolver los problemas de la geometría del espacio por medio de operaciones efectuadas en un plano y representar en él las figuras de los sólidos.
- Geometría proyectiva: la que trata de las proyecciones de las figuras sobre un plano.
Formas geométricas
Clasificación de las formas geométricas más elementales: Formas geométricas planas:
- Recta
- Polígonos
- Las secciones cónicas
Formas geométricas espaciales:
- Superficies regladas:
- Poliedros Regulares:
- Piramide
- Cuña
- Prisma
- Superficies de revolución:
- Cilindro
- Cono
- Esfera
- Elipsoide
- Paraboloide
- Hiperboloide
- Superficies no regladas
Aplicaciones
Toda disciplina que requiera la representación de elementos en una superficie plana (papel) encontrará, en la Geometría Descriptiva, un gran aliado. Es por esto que la Geometría Descriptiva se encuentra en todos los planes de estudios de Ingeniería, Arquitectura, Diseño, Topografía, entre otras. Una parte de ella estudia la Proyección Acotada, en la cual se basan los planos topográficos y de obras públicas, los cuales son trazados e interpretados normalmente por topógrafos.
Como asignatura de estudio obligatorio en las escuelas de ingeniería y arquitectura del mundo entero, el estudio de la Geometría Descriptiva persigue el desarrollo intelectual del estudiante en dos campos distintos pero complementarios: la comprensión del espacio tridimensional que rodea al individuo y el desarrollo de una estructura de pensamiento lógica, lo cual permite al profesional sentar las bases de otras disciplinas, como la mecánica de cuerpos rígidos, deformables y fluidos, enfrentando, al mismo tiempo, los problemas específicos de su área según un enfoque heurístico, no memorístico, de la realidad objeto de estudio.
Pudiera afirmarse que la Geometría Descriptiva es al ejercicio profesional del diseñador lo que la gramática es al idioma (palabras de Harry Osers). Como medio de expresión, requiere de una claridad y rigurosidad excepcional. Bien dice el refrán: una imagen dice más que mil palabras.
Geometría de incidencia
Una geometría es una estructura algebraica con al menos tres tipos de axiomas:
- ordenación
- incidencia
- congruencia
- Se llama geometría de incidencia a aquella estructura que carece de axiomas de congruencia. Entre otras cosas, la falta de estos axiomas nos impedirá comparar segmentos y establecer una métrica
Topología geométrica
La topología geométrica (topología de dimensiones bajas) es el área de la topología y la topología algebraica que estudia problemas geométricos, topológicos y algebraicos que surgen en el estudio de variedades de dimensiones menores que 5, espacios localmente homeomorfos a los espacios euclídeos, desde dimensión cero hasta la cuarta. Sus métodos están inspirados en la geometría y la topología de fenómenos físicos inclusive relativistas y cuánticos e idealizaciones abstractas modernas sobre el concepto de dimensiones: destacadamente y prominentemente, en tres y cuatro dimensiones.
Para ésta ciencia -que estudia las variedades y los encajes y encajes propios entre ellas-, estos son algunos de los temas representativos de esta ciencia: la teoría de nudos; clasificación de 3 y 4-variedades; Complementos de nudos en la n-esfera, Sn; TQFT.
La topología de dimensiones bajas (como también se le conoce) es considerada una ciencia de una gran interactividad entre todas la ramas de la matemática y con otras de la física. Una de las cuestiones importantes de esta rama (recién nresuelta por Perelman del 2006) es la célebre Conjetura de Poincaré, tanto como la conjetura de geometrización de Thruston.
Tópicos
- curva: Parametrización de un camino diferenciable entre dos puntos en algún espacio
- trayectoria: Casi como una curva pero no necesariamente diferenciable, sólo se pide continuidad
- circunferencia o 1-esfera: cualquier trayectoria, camino o curva cerrada simple.
- grupo fundamental: Functor de la topología algebraica que asigna a un espacio, X, su grupo fundamental π1(X)
- nudo: En el espacio X, es un subconjunto K de X, que es homeomorfo a la uno-esfera
- enlace: Conjunto de componentes conexas, cada componente homeomorfo a S1
- trenza (braid): Conjunto unidimensional que tiene el tipo homotópico de un wedge de circunferencia
- grupo de trenzas (braid group)
- Nudo tórico: curva cerrada simple en la superficie del toro
- superficie: La cáscara de objetos tridimensionales. Objetos localmente homeomorfos a

- esfera:
- toro (matemáticas):
- plano proyectivo: Espacio bidimensional construido apartir de identificar la frontera de una banda de Möbius y la frontera de un disco
- botella de Klein: Espacio que se crea, al pegar la frontera de dos bandas de Möbius
- aro o cilindro: I-bundle trivial sobre la 1-esfera
- banda de Möbius: Fibrado no trivial por intervalo sobre un círculo (I-bundle over S¹)
- Característica de Euler: Igual a número de vertices menos número de lados más número de caras. Es invariante al poner más vertices y por ende lados y caras
- Plano complejo:

- Plano cartesiano:

- Curvatura de superficies: Concepto de medida de como se curvan las superficies localmente, teniendo como patrón la esfera de radio r que se curva localmente 1/r² en cada uno de sus puntos. Observe que entre más grande el radio, la curvatura tiende a cero (que es la curvatura del plano). Dicho de otra manera: un plano es como una esfera de radio infinito.

Esquema simplicial de una tres-variedad hiperbólica

Celebridades de la topología de dimensiones bajas.
Geometría sagrada
La Geometría sagrada es un concepto planteado por el esoterismo y el gnosticismo para fundamentar la manera en que crea Dios. La creencia básica es que las razones geométrica y matemática, la armonía y la proporción, se encuentran en la cosmología, la musica, y las bellas artes en general.
Fundamentos de Diseño

Cilindro proyectado en dos planos
En todo diseño se tienen en cuenta cuatro componentes, lo conceptual, lo visual, lo relacional y lo práctico. Son elementos conceptuales aquellos que no son visibles: Son el punto, la línea, el plano y el volumen. Cuando los elementos conceptuales se hacen visibles, adquieren forma.
Las figuras geométricas
La palabra forma se confunde con figura, no obstante, una forma tri-dimensional puede tener múltiples figuras bi-dimensionales, cuando se la ve sobre una superficie lisa. La forma es entonces la apariencia visual total de un diseño y se identifica por su figura, tamaño, color y textura. La geometría descriptiva ha sido la encargada de la representación gráfica en superficies bidimensionales, de resolver los problemas del espacio en los que intervienen puntos, líneas y planos. Mediante proyecciones , translada los puntos de una figura a una superficie. Tal rama de la geometría resume la teoría del dibujo técnico.
.
El número Pi
El numero pi es la relación entre la longitud de la circunferencia y su diámetro.
La sección áurea
El número áureo y la sección áurea están presentes en todos los objetos geométricos regulares o semiregulares en los que haya simetría pentagonal, pentágonos o aparezca de alguna manera la raíz cuadrada de cinco.
- Relaciones entre las partes del pentágono.
- Relaciones entre las partes del pentágono estrellado, pentáculo o pentagrama.
- Relaciones entre las partes del decágono.
- Relaciones entre las partes del dodecaedro y del icosaedro.
Los sólidos platónicos
Para Platón, hay cinco sólidos tridimensionales de aristas, ángulos y caras iguales, tales sólidos platónicos son: el tetraedro, el cubo, el octaedro, el icosaedro y el dodecaedro.Esta exposición la hace en su díalogo el Timeo, en el que plantea que de la quinta combinación, (dodecaedro) Dios se sirvió para trazar el plano del universo.[1]
Interpretación
Para Blavatsky la geometría es la quinta llave que permite interpretar la vida, las cuatro primeras son: La fisiológica, la sicológica, la astrológica y la metafísica, la sexta es la simbólica y la séptima la matemática.[2]
Clave fisiológica
Desde la fisiología la aplicación de la geometría se puede encontrar en el Hombre vitruviano propuesto por Leonardo da Vinci. Cuando el perímetro son iguales, se produce la relación pi. Para Fritjof Capra los tres criterios clave para la vida y sus teorías subyacentes son:
- El patrón de organización, como configuración de relaciones (forma, orden y cualidad) que determina las características esenciales del sistema.
- La estructura o la corporeización física (substancia, materia, cantidad) del patrón de organización del sistema.
- El proceso vital como actividad involucrada en la contínua corporeización física.
Rupert Sheldrake postula la existencia de los campos morfogenéticos, como agentes causales del desarrollo y mantenimiento de la forma biológica.[3]
Los siete chakras están ubicados en el cuerpo humano de forma armónica, mediante los cuales ascienden espirales energéticas formando un ángulo de 90 grados a medida que pasan de un chakra el siguiente.
Clave Psicológica
La Psicología de la Gestalt plantea la existencia de todos irreductibles como un aspecto clave de la percepción. Se perciben patrones perceptuales integrados, conjuntos organizados dotados de significado. Para Carl Jung , un Mándala es un arquetipo (Jung) que representa los contenidos de conciencia de una persona, la manera como codifica la luz del conocimiento.[4]
Clave astrológica
Desde la astrología la división del zodíaco en doce partes, permite la comprensión del proceso de la vida, y se resume en tres libros en los cuales estudian y aprenden tres tipos de seres humanos.
- El libro de la Vida. Las doce constelaciones. Para Iniciados.
- El libro de la Sabiduría. Los doce planetas. Para Discípulos.
- El libro de la Forma. Las doce jerarquías creadoras. Para la humanidad.
Por lo tanto, la astrología trata de la vida y las vidas , que animan los "puntos de luz" dentro de la vida universal.[5]
Clave metafísica
Desde la metafísica el símbolo más representativo es el cubo de Metatrón, ya que contiene la réplica tridimensional de cuatro de los cinco sólidos platónicos, a los que Pitágoras llamaba sólidos perfectos. En las Escuelas de Egipto, a estas cinco formas, más la esfera se les consideraba originarias de los cinco elementos primordiales:tierra, fuego, aire, agua y éter.[6]
Clave geométrica
Teniendo en cuenta la geometría, la vida se inicia como un óvulo o esfera, pasa a convertirse en un tetraedro, después en una estrella tetraédrica y posteriormente en un cubo, a continuación en una nueva esfera y termina en un corpúsculo tubular.
Clave simbólica
De acuerdo con la semiótica, un símbolo es la representación de una idea. Para Djwhal Khul la representación del punto, la línea, el triángulo, el cuadrado, la cruz, el pentágono y el círculo, significa el reconocimiento de un vínculo con el conocimiento que ha determinado el desarrollo hasta la fecha. Plantea que en todas las razas hay siete formas análogas y actualmente son veintiuno los símbolos básicos que en forma geométrica encierran los conceptos de la civilización. Están adquiriendo forma el loto y la antorcha flamígera.[7]
La esfera giratoria de materia puede ser representada empleando los mismos símbolos generales cósmicos que se utilizan para representar la evolución:
- El círculo representa el límite de la materia indiferenciada.
- La circunferencia con un punto en el centro representa la producción de calor en el corazón de la materia como un punto de fuego.
- La división del círculo en dos partes, marca la rotación activa y la iniciación del movimiento del átomo de la materia.
- La división del círculo en cuatro partes representa la cruz de brazos iguales del espíritu santo, personificación de la materia inteligente activa. Como símbolo astrológico representa el planeta Tierra.
- La Esvástica representa el fuego que se extiende de la periferia al centro en cuatro direcciones, que circula e irradia gradualmente alrededor de toda ella.[8]
Clave matemática
Leonardo Fibonacci fue el matemático que descubrió determinado orden en el crecimiento de las plantas. La secuencia es 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233... Si se divide un término de esta secuencia por el siguiente, repitiendo el proceso el número se va acercando a 1,6180339 (89/55), coincidiendo con el número áureo definido por Euclides. La causa de este modelo secuencial se encuentra en la espiral media dorada que gira sin principio ni fin.
En matemáticas, rosa polar es el nombre que recibe cualquier miembro de una familia de curvas de ecuación  por asemejarse a una flor de pétalos. Esta familia, también conocida como rhodoneas (del griego rhodon, rosa), fue estudiada por el matemático Luigi Guido Grandi, en torno al 1725, en su libro Flores Geometrici.[9 por asemejarse a una flor de pétalos. Esta familia, también conocida como rhodoneas (del griego rhodon, rosa), fue estudiada por el matemático Luigi Guido Grandi, en torno al 1725, en su libro Flores Geometrici.[9
|
|
 |
| |
 |
|
|
|
|
|
|
|
|
|